Cette page est une version électronique de l'article publié dans les actes de l'International Conference on Image and Signal Processing (ICISP'2001), Agadir, Morocco, May 2001.

Segmentation d'Images en Couleur par Classification Morphologique Non Supervisée

Thierry Géraud, Pierre-Yves Strub, Jérôme Darbon
Laboratoire de Recherche et Développement de l'EPITA
14-16 rue Voltaire, F-94276 Le Kremlin-Bicêtre cedex, France
{ thierry.geraud, pierre-yves.strub, jerome.darbon }@lrde.epita.fr
http://www.lrde.epita.fr

Abstract

In this paper, we present an original method to segment color images using a classification of the image histogram in the 3D color space. As color modes in natural images usually do not fit a well-known statistical model, we propose a classifier that rely on mathematical morphology and, more particularly, on the watershed algorithm. We show on various images that the expected color modes are correctly identified and, in order to obtain coherent region, we extend the method to make the segmentation contextual.

1 Introduction

La segmentation a pour but de déterminer les régions d'une image cohérentes à la fois spatialement et du point de vue de leur contenu. Une catégorie de méthodes de segmentation d'images s'appuie sur une classification : les points de l'image sont des individus que l'on souhaite regrouper en classes. Pour cela, on considère que l'histogramme de l'image est un espace des caractéristiques de ces individus. Dans le cas des images en couleur, un nombre important de points qui sont de couleurs très proches produit une zone de valeurs élevées dans l'histogramme. D'un point de vue statistique, cette zone traduit la présence d'un mode de couleurs dans l'image. L'histogramme réduit à cette zone permet un calcul approximatif de la fonction de densité de probabilité (FDP) associée à ce mode. L'histogramme complet traduit la somme des FDP s ; cette somme est la fonction de densité de probabilité globale (FDPG). Les classifieurs statistiques prennent pour hypothèse que chaque FDP suit un modèle donné. Souvent, il s'agit d'une loi gaussienne ou multi-gaussiennes si l'espace des caractéristiques est de dimension supérieure ou égale à 2. Citons par exemple le classifieur proposé récemment par Frigui et Krisnapuram [2] qui réussit même à prendre en compte la superposition des modes dans l'espace des caractéristiques.

Cependant, dans le cas d'images en couleur quelconques, l'hypothèse de modes multi-gaussiens s'avère généralement très éloignée de la réalité. L'utilisation de classifieurs statistiques classiques s'en trouve alors peu justifiée. Une autre approche permettant d'identifier les modes d'un histogramme s'appuie sur l'aspect morphologique de l'histogramme et des techniques de morphologie mathématique [8] peuvent être utilisées. Cet article propose un classifieur morphologique non supervisé qui s'appuie sur l'algorithme de la ligne de partage des eaux (LPE) proposé par Vincent et Soille [9]. La LPE est appliquée dans l'espace des caractéristiques afin d'obtenir une segmentation de l'image. Cette méthode contraste donc avec les méthodes de segmentation par la LPE dans l'espace de l'image [6,3].

L'organisation de cet article est la suivante. La section 2 présente un état de l'art des méthodes de classification morphologique. La section 3 explique la méthode de classification morphologique non supervisée par LPE que nous proposons et donne ses propriétés. La section 4 commente les résultats que nous avons obtenus avec cette méthode. Enfin, la section 5 conclut cet article et discute des perspectives que laisse envisager la méthode proposée.

Nota bene : les images utilisées ou produites dans cet article ainsi que les résultats obtenus sur d'autres images de test sont disponibles sur l'Internet à partir de l'adresse http://www.lrde.epita.fr/download/.

2 État de l'art des classifieurs morphologiques

Tous les classifieurs morphologiques considèrent la FDPG comme une image numérique à valeurs entières afin de pouvoir analyser l'allure de la FDPG à l'aide de traitements d'images.

Dans [5], Postaire et al. propose un classifieur morphologique très simple qui utilise la morphologie mathématique binaire : la FDPG est seuillée pour obtenir une image binaire où l'objet correspond aux valeurs suffisamment élevées de densité donc au cur des modes ; une fermeture morphologique est appliquée pour régulariser la forme des objets ; enfin, un étiquetage de composantes connexes permet de distinguer les différents modes. Malheureusement, cette classification tire très peu parti de la forme ``à niveaux'' de la FDPG. De plus, un mode peu représenté, c'est-à-dire de faible probabilité a priori, disparaît avec le seuillage, même lorsque ce mode est bien isolé dans l'espace des caractéristiques.

Afin de palier ces défauts, Zhang et Postaire [10] proposent de traiter l'image à niveaux de la FDPG avant d'effectuer le seuillage. Le pré-traitement est un filtrage morphologique dépendant de la convexité du paysage de la FDPG qui a pour but d'augmenter la séparabilité des modes en creusant les vallées. Seulement, le relief initial entre deux modes doit déjà être suffisamment prononcé pour que les modes soient effectivement bien séparés.

Notons que les deux méthodes précédentes posent un problème lors de la segmentation finale de l'image originale. En effet, les modes sont identifiés sous la forme de composantes connexes dans l'espace des caractéristiques mais aucun partitionnement de cet espace n'est fourni ; dès lors, le vecteur caractéristique d'un point de l'image originale peut n'appartenir à aucune composante et l'affectation d'une classe à ce point n'est pas triviale. La méthode suivante résout ce problème.

Park et al. proposent une méthode beaucoup plus élaborée [4] : l'image de la FDPG est tout d'abord traitée par une différence de gaussiennes ; un seuillage de cette image de différence fournit une image binaire qui met en évidence les modes de l'histogramme original. À ce stade de la méthode, sur l'image de test dans [4], l'affectation d'une classe est impossible pour 30% des points de l'image à segmenter ce qui est dû au très fort étalement des occurrences dans l'histogramme 3D pour des images en couleur quelconques. Pour palier à ce problème, l'image binaire des modes est encore traitée. Une fermeture régularise la forme des modes ce qui se traduit par un double effet de bouchage et de fusion de ces derniers. Enfin, une dilatation augmente l'étendu de leur support . À l'issue de cette étape, l'étiquetage des points de l'image en couleur a lieu mais il reste encore des points non classifiables directement, leur couleur n'appartenant pas à un mode de l'espace des caractéristiques (leur couleur est un point du fond de l'image binaire qui représente l'espace caractéristique) ! Ces points sont finalement affecter à la classe la plus proche du point de vue de leur couleur.

L'utilisation comme classifieur de l'algorithme de la ligne de partage des eaux (LPE) a été mise en évidence par Soille [7]. La LPE fournit un partitionnement d'une image en bassins tel que chaque bassin entoure un minimum local de l'image et tel que les frontières entre bassins passent par les crêtes de l'image. Sur l'histogramme inversé d'une image, les modes se traduisent par des cuvettes et sont séparés par des crêtes. Cependant, calculer directement la LPE sur l'histogramme inversé produirait un sur-partitionnement dû à la présence de minima locaux parasites. Afin d'éviter cela, l'histogramme original est pré-traité. Tout d'abord, les pics de plus forte dynamique sont sélectionnés pour définir des marqueurs. Ensuite, une reconstruction morphologique de l'histogramme par dilatation à partir de ces marqueurs garantit que les seuls maxima locaux correspondent aux pics sélectionnés.

La LPE permet de s'affranchir du problème de points non classifiables car son résultat est un étiquetage en classes de tout l'espace des caractéristiques. En revanche, appliquer telle quelle la méthode de Soille à des images en couleur n'est pas envisageable car leurs histogrammes 3D ne sont généralement pas assez denses et les modes ne sont pas suffisamment apparents.

3 Classification par LPE

3.1 Préambule

La méthode que nous proposons considère l'histogramme 3D $H_I$ d'une image $I$ en couleur. Le vecteur caractéristique d'un point $p$ de l'image est le vecteur de ses composantes rouge-vert-bleu, $I(p)=(r,v,b)$. Dans cet article, certaines images 3D associent à chaque point/couleur $c$ un scalaire ; par exemple, c'est le cas de l'histogramme $H_I$ : $H_I(c)\in\mathop{\hbox{\mit I\kern-.2em N}}\nolimits$. Les autres images 3D associent à chaque point/couleur une étiquette.

Afin de visualiser le contenu d'une image 3D, $T$, nous aurons recours à une projection 2D sur le plan rouge-vert : $T_{RV}$ (le choix de ce plan est justifié car les composantes rouge et vert sont faiblement corrélées).

Lorsque $T$ est une image de scalaires, la projection vérifie :

$$T_{RV}(r,v) = \frac{\sum_{b} T(r,v,b)}{N} \mbox{~~~~~où~} N = \max_{(r,v)} \sum_{b} T(r,v,b).$$

Dans les figures montrant cette projection, les points $(r,v)$ tels que $T_{RV}(r,v) = 1$ apparaissent en blanc, les points de valeur 0 apparaissent en noir et ceux de valeurs intermédiaires en gris.

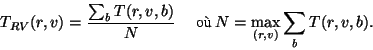
Lorsque $T$ est une image d'étiquettes, notons $e$ une étiquette ; $\delta$ étant le symbole de Kronecker, formons :

$$\begin{array}{l} h_{RV}((r,v),e) = \displaystyle\sum_{b} H_I... ..., \displaystyle\max_{e \neq e_1} \, h_{RV}((r,v),e) \end{array}$$

Soit une fonction $f$ telle que $f(e)\in \, ]0,1[$. La projection de $T$ vérifie :

$$T_{RV}(r,v) = \left\{ \begin{array}{ll} 1 & \mbox{si~~} \dis... ...1(r,v) > e_2(r,v) + 5 \\ 0 & \mbox{sinon}. \end{array}\right.$$

Comme précédemment, 1 apparaît en blanc, 0 en noir, et les valeurs intermédiaires en gris. Ainsi, un point blanc en $(r,v)$ signifie qu'il y a très peu de points de couleur $(r,v,b)\;\forall\,b$ dans l'image originale ; un point noir signifie qu'il y a ambiguïté pour l'étiquette majoritaire selon $T$ des points de couleur $(r,v,b)\;\forall\,b$ dans l'image originale.

3.2 Description de la méthode proposée

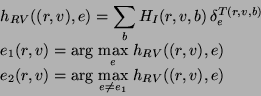
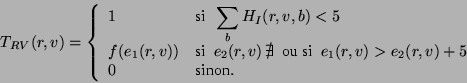
Nous donnons ici une description des différentes étapes de la méthode de classification morphologique non supervisée que nous proposons. Nous en illustrons les différentes étapes sur l'image en couleur peppers comprenant 512$\times$512 points RVB, chaque composante de couleur étant codée sur 8 bit ; Cf. la figure 1 (a).

Figure 1. Image peppers illustrant la méthode de classification morphologique proposée ici ; (a) est l'image originale, (b) représente son histogramme 3D dans l'espace rouge-vert-bleu.

(a)

 


(b)

1. La première étape consiste à calculer l'histogramme 3D de l'image en couleur. Il est représenté en figure 1 (b) sous la forme d'un nuage de points dont la densité locale est proportionnelle aux valeurs d'occurrence. Nous pouvons observer que l'hypothèse de modes multi-gaussiens n'est effectivement pas justifiée. Nous modifions alors la dynamique de l'histogramme suivant :
   
   $$\forall \, c, \; H_2(c) = M - \, \log( 1 + H_I(c) ) \mbox{~~~~~où~} M = \max_c \, \log( 1 + H_I(c) ).$$
   
   
   Cette prise de logarithme a pour but de rehausser les faibles valeurs de l'histogramme. Elle est suivie d'une inversion afin que les maxima de l'histogramme deviennent des minima. La projection 2D du résultat $H_2$ est donnée en figure 2 (a).

   Figure 2. Différentes étapes de la classification morphologique illustrées par des projections 2D (rouge-vert) des images 3D ; (a) représente l'histogramme après changement de dynamique, $H_2$ ; (b), après filtrage passe-bas, $H_3$ ; (c), après saturation et fermeture, $H_4$ ; et (d), après partitionnement par la LPE, $W$.

   
   (a)

   
   (b)

   
   (c)

   
   (d)

2. La seconde étape a pour but de régulariser $H_2$. Pour cela, un filtrage gaussien 3D d'écart-type $\sigma=3$ est appliqué sur $H_2$ (cette valeur d'écart-type, fixée empiriquement, s'avère satisfaisante sur l'ensemble des images de test utilisées). Ce filtrage lisse l'histogramme et élimine bon nombre de minima locaux. Du fait de la séparabilité de ce filtre, son exécution est rapide. La projection 2D du résultat $H_3$ est donnée en figure 2 (b).

3. Avant d'exécuter l'algorithme de la LPE, nous devons nous débarrasser de minima trop locaux. Ils se trouvent principalement dans les régions de fortes valeurs (les régions blanches dans la figure 2 qui correspondent du point de vue de l'image en couleur originale aux couleurs extrêmement peu représentées). Nous saturons donc le niveau de ces régions ; le seuil de saturation est la valeur médiane des valeurs $H_3(c) \neq 0$. Enfin, une fermeture morphologique permet de supprimer des minima locaux résiduels. Grâce à l'étape précédente, l'élément structurant n'a pas besoin d'être de grande taille ; nous avons pris l'élément correspondant à la 18-connexité. La projection 2D du résultat $H_4$ de cette étape est donnée en figure 2 (c).

4. L'algorithme de la LPE est alors exécuté et donne l'image $W$ d'étiquettes. Afin d'obtenir un partitionnement complet de l'espace des caractéristiques, nous avons opté pour une version ``connectée'' de l'algorithme [1], c'est-à-dire, telle qu'aucun point de l'espace n'a au final l'étiquette SHED. Pour chaque bassin $w_i$, nous calculons la couleur moyenne suivant :
   
   $$\overline{c_i} = \frac{ \sum_{c\in w_i} \, H_I(c) \, c} {\sum_{c\in w_i} \, H_I(c)}$$
   
   
   La projection 2D de $W$ est donnée en figure 2 (d).

5. La segmentation $S$ de l'image originale s'appuie sur le partitionnement de l'espace des couleurs :
   
   $$S(p) = \overline{c_{i(p)}} \mbox{~~~~~où~} i(p) \mbox{~est tel que~} I(p) \in w_{i(p)}.$$
   
   
   Le résultat final est donné en figure 3 (a).

3.3 Propriétés

La méthode que nous proposons possèdent plusieurs propriétés théoriques fortes. Le résultat de l'algorithme de la LPE, $W$, obtenu à l'issue de l'étape 4, est invariant par rapport aux transformations suivantes de l'histogramme 3D original, $H_I$, calculé au début de l'étape 1.

• Modification de dynamique par une fonction $f$ croissante :  $H'_I(c) = f( \,H_I(c)\,) \; \Rightarrow \; W'(c) = W(c).$
• Application d'une transformation linéaire $L$ sur les couleurs :  $H'_I(c') = H_I(\,L\,c\,) \; \Rightarrow \; W'(c') = W(\,L\,c\,).$
  Cette propriété n'est généralement pas vérifiée pour les classifieurs statistiques comme le montre Soille [8] (section 10.2.3).
• Application d'une translation $T$ sur les couleurs :  $H'_I(c')=H_I(\,T(c)\,) \; \Rightarrow \; W'(c')=W(\,T(c)\,).$
• Application d'une rotation $R$ sur les couleurs :  $H'_I(c')=H_I(\,R(c)\,) \; \Rightarrow \; W'(c')=W(\,R(c)\,).$

4 Résultats

Le résultat $S$ de la classification morphologique par LPE sur l'image de test peppers est donné en figure 3 (a). Pour un classifieur non-contextuel, nous pouvons remarquer que les régions obtenues sont relativement bien homogènes spatialement.

Toutefois, si une segmentation contextuelle est nécessaire, une variante très simple de l'étape 5 est la suivante. Appliquer l'algorithme de la LPE connectée à l'image en couleur originale ; pour cela, calculer l'image de la valeur absolue du gradient, la fermer morphologiquement par un petit élément structurant (c8), puis calculer la LPE connectée. Notons $W^I$ l'image de la LPE connectée issue de $I$ ; notons $w^I_j$ son $j$ème bassin et $\overline{c^I_j}$ la couleur moyenne des points de ce bassin dans $I$. Soit $j(p)$ l'indice du bassin de $W^I$ auquel $p$ appartient ( $p \in w^I_{j(p)}$). Soit $i'(p)$ l'indice du bassin de $W$ qui contient la couleur moyenne de $w^I_{j(p)}$ (c'est-à-dire, $\overline{c^I_{j(p)}} \in w_{i'(p)}$). La segmentation s'effectue alors suivant :

$$S^I(p) = \overline{c_{i'(p)}}$$

L'algorithme de la LPE dans l'espace (2D) de l'image en couleur fournit une sur-segmentation mais le nombre de couleurs attribuées aux bassins 2D est restreinte par le nombre de bassins obtenus dans l'espace (3D) des caractéristiques. In fine, des bassins 2D adjacents sont souvent de même couleur et forment ainsi de larges régions. La figure 3 (b) montre le résultat de la segmentation de l'image de test.

Figure 3. Résultat de la classification morphologique pour l'image de test peppers ; (a) avec l'attribution non contextuelle d'une couleur à chaque point, (b) idem mais pour chaque bassin obtenu par LPE dans l'espace de l'image.

(a)

(b)

Nous avons appliqué la classification morphologique à un jeu d'une dizaine d'images en couleur (l'ensemble des résultats est disponible sur l'Internet à partir de l'adresse http://www.lrde.epita.fr/download/). Une illustration de plusieurs classifications est donnée en figure 4 et nous donnons ici quelques observations remarquables. L'image house, très classique, est facile à segmenter ; le comportement du classifieur morphologique donne effectivement le résultat attendu. L'image jbeanc contient des haricots peints de couleurs différentes mais dont la surface présente une spécularité importante ; l'histogramme ne se prête donc pas à une classification mais la segmentation est de très bonne qualité. L'image tiffany a une piètre dynamique des couleurs ; contrairement au reste de l'image, les lèvres, qui représentent peu de points dans l'image, sont violacées et donnent lieu à une classe à part entière (ce qu'un classifieur ``classique'' a dû mal à réaliser). Remarquons enfin que, grâce au filtrage passe-bas, le classifieur morphologique se comporte correctement sur des images qui sont mal quantifiées (par exemple, girl).

Figure 4. Résultats $W$ en projection 2D de la classification morphologique par LPE (b) sur 3 images de test ; nous pouvons constater que non seulement les modes de couleurs, présents dans l'histogramme $H_2$ (a), sont bien reconnus mais aussi que la forme des bassins est bien adaptée à celle des données.

house (a)

house (b)

lena (a)

lena (b)

jbeanc (a)

jbeanc (b)

5 Conclusion et perspectives

Dans cet article, nous proposons une méthode de classification morphologique non supervisée pour les images en couleur (section 3). L'utilisation de la morphologie mathématique comme outil de classification est encore peu classique et nous montrons en particulier que l'algorithme de la LPE s'avère un classifieur bien adapté pour les images en couleur. La méthode proposée fournit de très bons résultats ; ils s'expliquent par le fait que l'on ne puisse pas considérer que les modes de couleur soient d'une forme statistique donnée dans ces images.

La classification dans l'espace des couleurs ne suffit cependant pas pour obtenir des segmentations pertinentes d'images en couleur. Nous avons présenté ici (section 4) une façon très simple de garantir, à l'issue de la classification, la cohérence spatiale des régions de l'image segmentée. Nous pouvons imaginer cependant d'appliquer d'autres méthodes de régularisation, plus élaborées. Par exemple, la classification morphologique peut servir d'étape d'apprentissage des modes ``statistiques'' de couleur et une segmentation par classification markovienne peut alors être menée dans l'espace de l'image en couleur. Une perspective d'une toute autre nature est de continuer l'étude morphologique dans l'espace des couleurs pour déduire de la forme des modes les connections en queue de comète qui les relient et qui sont dues soit aux dégradés de couleurs dans l'image soit aux effets de mélange. Enfin, nous pouvons envisager une version plus rapide et moins gourmande en mémoire du classifieur morphologique en utilisant non plus un espace 3D des couleurs mais 3 projections 2D de cet espace.

Bibliography

1

A. Bieniek and A. Moga,
``An Efficient Watershed Algorithm Based on Connected Components'',
Pattern Recognition, 33(6), 2000, pp. 907-916.

2

H. Frigui and R. Krisnapuram,
``A Robust Competitive Clustering Algorithm with Applications in Computer Vision'',
IEEE Transactions on Pattern Analysis and Machine Intelligence, 21(5), May 1999, pp. 450-465.

3

K. Haris, S. N. Estradiadis, N. Maglaveras, and A. K. Katsaggelos,
``Hybrid Image Segmentation Using Watersheds and Fast Region Merging'',
IEEE Transactions on Image Processing, 7(12), 1998, pp. 1684-1699.

4

S.H. Park, I.D. Yun, and S.U. Lee,
``Color Image Segmentation Based on 3-D Clustering: Morphological Approach'',
Pattern Recognition, 31(8), 1998, pp. 1061-1076.

5

J.G. Postaire, R.D. Zhang, and C. Lecocq-Botte.
``Cluster Analysis by Binary Morphology'',
IEEE Transactions on Pattern Analysis and Machine Intelligence, 15(2), February 1993, pp. 170-180.

6

K. Saarinen,
``Color Image Segmentation by a Watershed Algorithm and Region Adjacency Graph Processing'',
In Proceedings of IEEE International Conference on Image Processing, vol. 3, Austin, TX, USA, November 1994, pp. 1021-1025.

7

P. Soille,
``Morphological Partitioning of Multispectral Images'',
Journal of Electronic Imaging, 5(3), 1996, pp. 252-265.

8

Soille, P.,
Morphological Image Analysis - Principles and Applications,
Springer-Verlag, 1999.

9

L. Vincent and P. Soille,
``Watersheds in Digital Spaces: an Efficient Algorithm Based on Immersion Simulations'',
IEEE Transactions on Pattern Analysis and Machine Intelligence, 13(6), June 1991, pp. 583-598.

10

R.D. Zhang and J.G. Postaire,
``Convexity Dependent Morphological Transformations for Mode Detection in Cluster Analysis'',
Pattern Recognition, 27(1), 1994, pp. 135-148.

About this document ...

This document was generated using the LaTeX2HTML translator Version 99.2beta6 (1.42)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.